Top-Down Parsing #

The section begins with a general form of top-down parsing, called recursive-descent parsing, which may require backtracking to find the correct -production to be applied. Later we'll introduce predictive parsing, a special case of recursive-descent parsing, where no backtracking is required. Predictive parsing chooses the correct -production by looking ahead at the input a fixed number of symbols, typically we may look only at one (that is, the next input symbol).

Recursive-Descent Parsing #

Consider the grammar

To construct a parse tree top-down for the input string , begin with the starting node , and the input pointer pointing to the first character from left to right of the input, i.e., .

1. Since has only one production, we use it to expand and obtain the tree of the lhs of the figure below.
2. The leftmost leaf, labeled , matches the first symbol of input , so we advance the input pointer to . Now, use the first alternative to obtain the tree of the middle of the figure below.
3. Since does not match , we report failure and go back to and retract the input pointer to seek for another alternative producing a match. The second alternative produces the tree of rhs of the figure below. The leaf and match to the second and the third symbols of respectively, we halt and annouce successful completion of parsing.

Noted that a left-recursive grammar can cause a recursive-descent parser, even one with backtracking, to go into an infinite loop. That's why we've talked about the elimination of left recursion. Also, the backtracking is not an efficient way to construct a parse tree, thus we shall see how to predict the right alternative below.

FIRST Set #

Why FIRST #

Consider the production rule

Assume the input string is . Scanning from left to write, upon reading , we know that may be applicable but only if produces a string led by . Therefore, we need to know what comes first in , i.e. .

In this case, , so we can tell that is applicable and use the production rule to build the following parse tree.

Rules for FIRST set #

To compute for all grammar symbol , apply the following rules until no more terminals or can be added to any FIRST set.

1. If is a terminal, then .
2. If is a nonterminal and is a production for some
   • Place in if for some , is in , and is in all of , i.e., .
   • Add to if is in for all .
3. If is a production, then add to .

A simple example #

Consider the production rules below

Find the FIRST sets for the nonterminals

FIRST(F) = {(}
FIRST(F) = {(, id}

FIRST(E') = {+}
FIRST(E') = {+, ε}

FIRST(T') = {*}
FIRST(T') = {*, ε}

FIRST(T) = FIRST(F) = {(, id}
FIRST(E) = FIRST(T) = {(, id}

FOLLOW Set #

Why FOLLOW #

Consider the production rule

Suppose the string to parse is . Scanning from left to write, upon reading , we know that may be applicable but only if can vanish and the character follows is . That's why we need to know what follows , i.e.

In this case, and the current input (after scanned ) is . Hence the parser applies this rule and generate the following parse tree

Rules for FOLLOW set #

To compute for all nonterminals , apply the following rules until nothing can be added to any FOLLOW set.

1. Place in , where is the start symbol and is the input right endmarker.
2. If there is a production , then everything in except is in .
3. If there is a production , or a production , where contains , then everything in is in .

A simple example #

Continue the example above

Find the FOLLOW sets for the nonterminals

FOLLOW(E) = {$}
FOLLOW(E) = {$, )}

FOLLOW(E') = FOLLOW(E) = {$, )}

FOLLOW(T) = FIRST(E') - {ε} = {+}
FOLLOW(T) = {+} ∪ FOLLOW(E) = {+, $, )}

FOLLOW(T') = FOLLOW(T) = {+, $, )}

FOLLOW(F) = FIRST(T') - {ε} = {*}
FOLLOW(F) = {*} ∪ FOLLOW(T) = {*, +, $, )}

LL(1) Grammars #

Predictive parsers, that is, recursive-descent parsers needing no backtracking, can be constructed for a class of grammars called LL(1).

1. The first "L" in LL(1) stands for scanning the input from left to right,
2. The second "L" for producing a leftmost derivation
3. The "1" for using one input symbol of lookahead at each step to make parsing action decisions.

Definition of LL(1) grammars #

A grammar is LL(1) if and only if whenever are two distinct productions of , the following conditions hold:

1. No left-recursion or ambiguity
2. For no terminal do both and derive strings beginning with .
   • Equivalent to that and are disjoint sets.
3. At most one of and can derive the empty string.
4. If , then does not derive any string beginning with a terminal in , and vice versa.
   • Equivalent to that if is in , then and are disjoint sets, and vice versa.

Nonrecursive Predictive Parsing #

Construction of a predictive parsing table #

For each production of the grammar, do the following:

1. For each terminal in , add to
2. If is in , then for each terminal in , add to . If is in and is in , add to as well.

Finally, set to error if there's no production at all.

Use the same grammar above for example, but we'll use the standard BNF for a clearer view

For E -> TE'
    1.  M[E, (]  = E -> TE'
        M[E, id] = E -> TE'

For E' -> +TE'
    1.  M[E', +] = E' -> +TE'

For E' -> ε
    2.  M[E', )] = E' -> ε
        M[E', $] = E' -> ε

For T -> FT'
    1.  M[T, (]  = T -> FT'
        M[T, id] = T -> FT'

For T' -> *FT'
    1.  M[T', *] = T' -> *FT'

For T' -> ε
    2.  M[T', +] = T' -> ε
        M[T', )] = T' -> ε
        M[T', $] = T' -> ε

For F -> (E)
    1.  M[F, (]  = F -> (E)

For F -> id
    1.  M[F, id] = F -> id

PREDICT sets and LL(1) verification #

In some literature, the predictive parsing table can be viewed as PREDICT sets. For each production of the grammar, add into if is .

We can further combine the 2^nd and 4^th conditions in the definition of LL(1) grammars into the examination of PREDICT sets. LL(1) contains exactly those grammars that have disjoint PREDICT sets for productions that share a common left-hand side. That is, at most one production can be added into each entry in the predictive parsing table .

Table-driven predictive parsing #

Model of a table-driven predictive parser

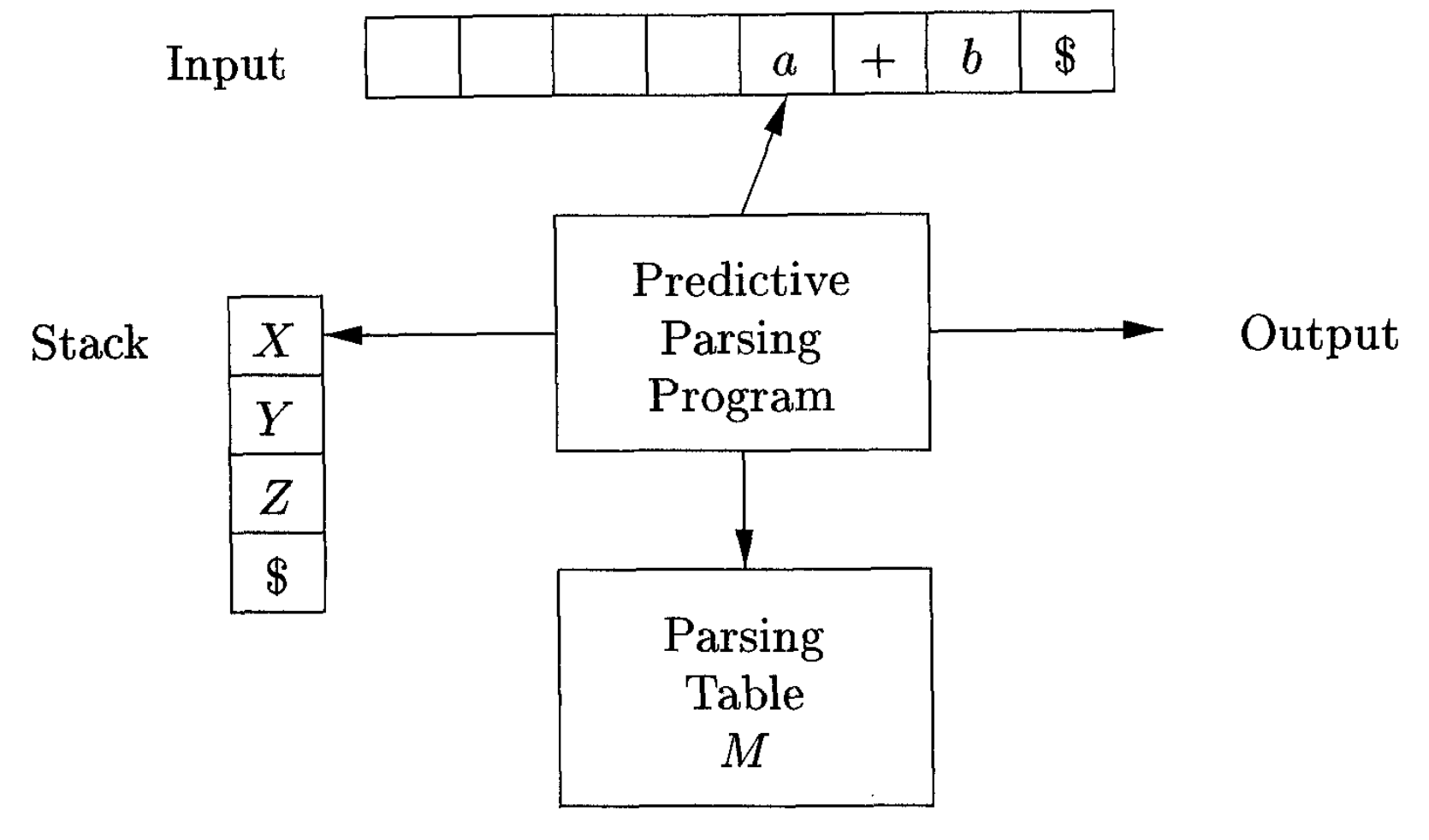
Image credit to Compilers: Principles, Techniques, and Tools 2nd Edition

• Input: A string and a parsing table for grammar .
• Output: A leftmost derivation of or an error indication.

Initially, the parser is in a configuration with in the input buffer and the start symbol of on top of the stack, above .

• Set the input pointer to point to the first symbol of
• Set to the top stack symbol and while do the following

1. If is , pop the stack and advance .
   • Else if is a terminal or is an error entry ,error out.
   • Else if
     1. Output the production
     2. Pop the stack
     3. Push onto the stack, with on top
2. Set to the top stack symbol.

Example #

Continue from above

Moves made by a predictive parser on input